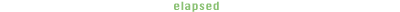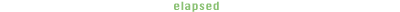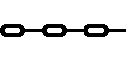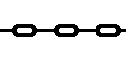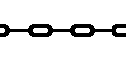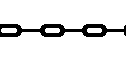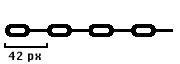Waveforms in games
Introduction
In this tutorial, we're going to look at some common periodic waveforms and their application in games.
Waveforms
Sine wave

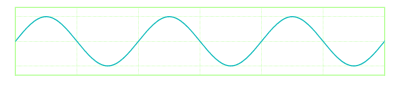
The sine wave describes a smooth repetitive oscillation.
The following code calculates the magnitude of the wave (a) given the elapsed time and the period.
The value of a is between 0 and 1.
local t = elapsed/period
local a = math.sin(t*math.pi*2)
a = (a + 1)/2
In the early days, programmers would often generate sound effects for their games procedurally as opposed to using pre-recorded samples.
The sine wave could be used to produce simple effects like the jumping sound in the original Super Mario Bros.
function newSinewave(frequency, samplerate, duration)
-- default duration is one wave period
duration = duration or 1/frequency
local samples = math.floor(duration*samplerate)
local data = love.sound.newSoundData(samples)
for i = 1, samples do
local v = (i - 1)*frequency/samplerate
v = math.sin(v*math.pi*2)
data:setSample(i, v)
end
return data
end
local data = newSinewave(100, 44100, 2)
local src = love.audio.newSource(data, "static")
src:setLooping(true)
love.audio.play(src)
Before the wave data buffer is loaded in a sound object we can do some cool stuff.
For example, we can iterate and modify the data buffer to apply a fade-in/out effect.
for i = 1, samples do
local v = (i - 1)*frequency/samplerate
v = math.sin(v*math.pi)
v = (i - 1)/samples*v -- fade
data:setSample(i, v)
end
Sawtooth wave

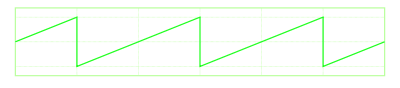
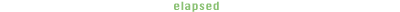
This wave looks like the teeth of a saw.
The following code calculates the magnitude of the wave (a) as a value between 0 and 1.
local t = (elapsed + period/2)%period
local a = t/period
One application of the sawtooth wave could be to produce seamlessly looping animations.
Let's take for example, the following animation of a chain being pulled:
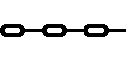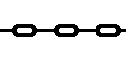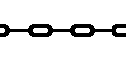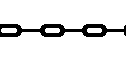
The basic technique involves creating a sprite with some pattern drawn onto it.
Then we update the X-position of the sprite based on a sawtooth wave.
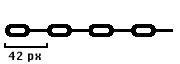
Suppose the distance between two links of the chain is 42 pixels.
This distance will serve as the amplitude of the wave.
The wave period (p) affects the rate of the animation.
local p = 0.5 -- wave period in seconds
local e = 0
function love.update(dt)
e = e + dt -- elapsed time in seconds
local t = (e + p/2)%p
sprite.x = t/p*42 -- update sprite position
end
Triangle wave

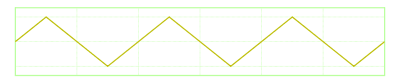
local t = (elapsed - period/4)%period
return math.abs(t*2 - period)/period
The triangle wave could be used in games to make moving platforms and such.
Waveforms in general are especially useful in physic-based games.
For example, joint motors in the Box2D library could be oscillated using waveforms to produce some very nice effects.
Square wave

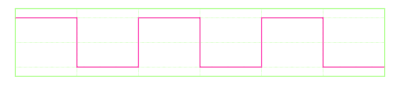
A square wave alternates at a steady frequency between fixed minimum and maximum values.
In the following example, the value of a is either 0 or 1.
local hp = period/2
local t = (elapsed + hp)%period
local a = math.floor(t/hp)
Square waves are often used to periodically toggle between two different states.
With square waves, for the first half of the wave period we are in an active state (1) and for the second half of the period we are in inactive state (0).
This ratio could be changed by introducing the "dutycycle" variable.
Duty cycle is the percent of time that an entity spends in an active state.
For simple square waves D is 0.5 or 50%.

The duty cycle (D) is defined as the ratio between the pulse duration and the period of a rectangular waveform.
local hp = period/2
local t = (elapsed + hp)%period
if t > period*dutycycle then
-- inactive state
else
-- active state
end
Tweening or easing
Some waveforms are particularly useful for visual effects known as "tweening" or "easing."
Here are some examples:
Linear
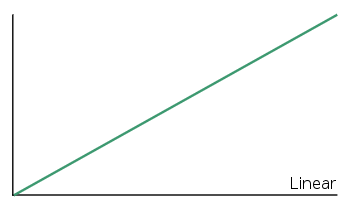
local linear = elapsed/period
Quadratic, cubic, quart and quint
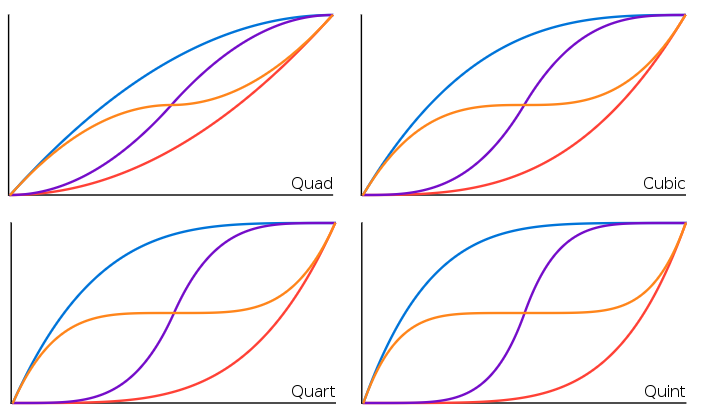
local quadratic = linear^2
local cubic = linear^3
local quart = linear^4
local quint = linear^5
Exponential
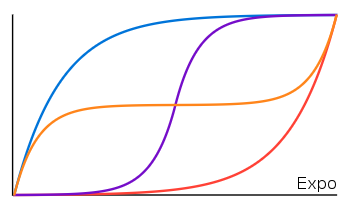
local expo = math.pow(2, 10*(linear - 1))
Circular
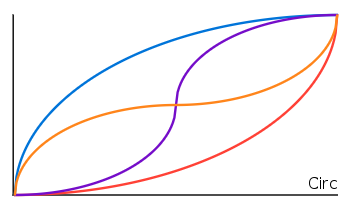
local circ = math.sqrt(1 - linear^2) - 1
Sine
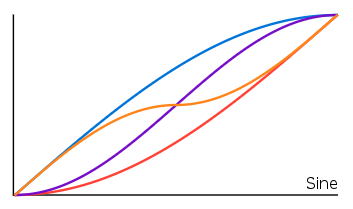
local sine = math.sin(linear*(math.pi/2))
Bounce
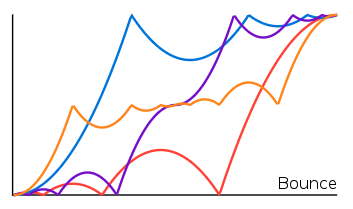
...
Back
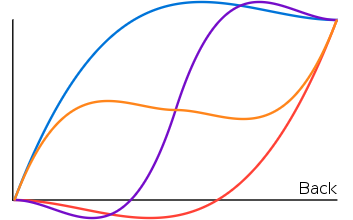
local s = s or 1.70158
local t = linear - 1
local back = (t*t*((s + 1)*t + s) + 1)
Elastic
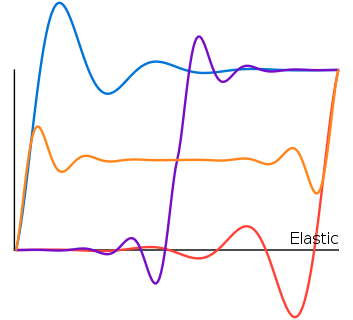
...