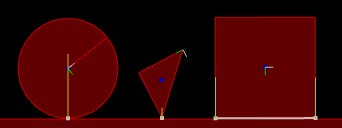
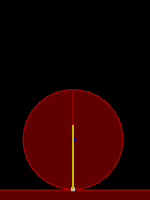
Three different contacts with the contact points shown in white
Left: circle with 1 contact (1 point)
Center: triangle with 1 contact (1 point, vertex to edge)
Right: rectangle with 1 contact (2 points, edge to edge)
Box2D is the library hiding under the hood of love.physics. In this tutorial, we'll learn how to use Box2D like a pro!
local reg = debug.getregistry()
local lg = love.graphics
-- World
function reg.World:draw()
local bodies = self:getBodies()
for _, v in ipairs(bodies) do
v:draw()
end
lg.setColor(1,0,0,1)
local joints = self:getJoints()
for _, joint in ipairs(joints) do
local x1, y1, x2, y2 = joint:getAnchors()
if joint.getGroundAnchors then
local x3, y3, x4, y4 = joint:getGroundAnchors()
lg.line(x1, y1, x3, y3, x4, y4, x2, y2)
else
lg.line(x1, y1, x2, y2)
end
end
end
-- Body
function reg.Body:draw()
local x, y = self:getPosition()
local r = self:getAngle()
lg.push()
lg.translate(x, y)
lg.rotate(r)
local fixtures = self:getFixtures()
for _, fixture in ipairs(fixtures) do
local shape = fixture:getShape()
shape:draw()
end
lg.pop()
end
-- Shape
function reg.CircleShape:draw()
local x, y = self:getPoint()
local r = self:getRadius()
lg.circle("line", x, y, r, 32)
lg.line(x, y, x + r, y)
end
function reg.PolygonShape:draw()
lg.polygon("line", self:getPoints())
end
function reg.ChainShape:draw()
lg.line(self:getPoints())
end
function reg.EdgeShape:draw()
lg.line(self:getPoints())
end
"b2draw" makes drawing our physics simulation super easy! However, Box2D is based on the metric system so some scaling may be required. A circle shape with a radius of 100 is simulated as if its radius is 100 meters. 100 meters is nearly the length of a football field and is probably not the ideal size to simulate a bouncing ball. To keep the simulation realistic, we need to stick to everyday-sized objects. For example, a soccer ball is around 0.1 meters in radius. Rendering such tiny shapes in an 800 by 600 window requires scaling your sprites or using a "camera." Alternatively you could use love.physics.setMeter.
local reg = debug.getregistry()
local lp = love.physics
local newBody = lp.newBody
function reg.World:newBody(x, y, t)
return newBody(self, x, y, t)
end
local destroyBody = reg.Body.destroy
function reg.World:destroyBody(b)
destroyBody(b)
end
local destroyJoint = reg.Joint.destroy
function reg.World:destroyJoint(j)
destroyJoint(j)
end
local newPolygonShape = lp.newPolygonShape
local newFixture = lp.newFixture
function reg.Body:newPolygon(...)
local s = newPolygonShape(...)
return newFixture(self, s)
end
local newRectangleShape = lp.newRectangleShape
function reg.Body:newBox(w, h, lx, ly, la)
lx, ly = lx or 0, ly or 0
la = la or 0
local s = newRectangleShape(lx, ly, w*2, h*2, la)
return newFixture(self, s)
end
local newCircleShape = lp.newCircleShape
function reg.Body:newCircle(radius, lx, ly)
lx, ly = lx or 0, ly or 0
local s = newCircleShape(lx, ly, radius)
return newFixture(self, s)
end
local newChainShape = lp.newChainShape
function reg.Body:newChain(vertices, loop)
local s = newChainShape(loop, vertices)
return newFixture(self, s)
end
local newEdgeShape = lp.newEdgeShape
function reg.Body:newEdge(x1, y1, x2, y2)
local s = newEdgeShape(x1, y1, x2, y2)
return newFixture(self, s)
end
local newRevoluteJoint = lp.newRevoluteJoint
function reg.World:newRevoluteJoint(a, b, x, y, cc)
return newRevoluteJoint(a, b, x, y, cc)
end
local newPrismaticJoint = lp.newPrismaticJoint
function reg.World:newPrismaticJoint(a, b, x, y, ax, ay, cc)
return newPrismaticJoint(a, b, x, y, ax, ay, cc)
end
local newDistanceJoint = lp.newDistanceJoint
function reg.World:newDistanceJoint(a, b, p1x, p1y, p2x, p2y, cc)
return newDistanceJoint(a, b, p1x, p1y, p2x, p2y, cc)
end
local newRopeJoint = lp.newRopeJoint
local sqrt = math.sqrt
function reg.World:newRopeJoint(a, b, p1x, p1y, p2x, p2y, l, cc)
if l == nil then
local lx, ly = p1x - p2x, p1y - p2y
l = sqrt(lx*lx + ly*ly)
end
return newRopeJoint(a, b, p1x, p1y, p2x, p2y, l, cc)
end
local newPulleyJoint = lp.newPulleyJoint
function reg.World:newPulleyJoint(a, b, p1x, p1y, p2x, p2y, p3x, p3y, p4x, p4y, ratio, cc)
return newPulleyJoint(a, b, p1y, p2x, p2y, p3x, p3y, p4x, p4y, ratio, cc)
end
local newGearJoint = lp.newGearJoint
function reg.World:newGearJoint(a, b, j1, j2, ratio, cc)
return newGearJoint(j1, j2, ratio, cc)
end
local newWeldJoint = lp.newWeldJoint
function reg.World:newWeldJoint(a, b, p1x, p1y, cc)
return newWeldJoint(a, b, p1x, p1y, cc)
end
local newFrictionJoint = lp.newFrictionJoint
function reg.World:newFrictionJoint(a, b, p1x, p1y, cc)
return newFrictionJoint(a, b, p1x, p1y, cc)
end
local newWheelJoint = lp.newWheelJoint
function reg.World:newWheelJoint(a, b, p1x, p1y, ax, ay, cc)
return newWheelJoint(a, b, p1x, p1y, ax, ay, cc)
end
local newMouseJoint = lp.newMouseJoint
function reg.World:newMouseJoint(a, x, y, mf)
local joint = newMouseJoint(a, x, y)
joint:setMaxForce(mf)
return joint
end
The code for creating new fixtures and shapes becomes much shorter and cleaner thanks to "b2access.lua." This is all achieved with barely any effect on performance.
require("b2draw")
require("b2access")
function love.load()
world = love.physics.newWorld()
body = world:newBody(100, 100)
fixture = body:newCircle(10)
end
function love.update(dt)
world:update(dt)
end
function love.draw()
world:draw()
end
accumulator = 0
interval = 1/60
maxframeskip = 10
function love.update(dt)
accumulator = accumulator + dt
accumulator = math.min(accumulator, maxframeskip*interval)
while accumulator >= interval do
world:update(interval)
accumulator = accumulator - interval
end
end
Note that when using accumulators, not all of "delta" will be used during a single cycle. Some people use this tiny left-over "delta" to interpolate while drawing:
function love.draw()
-- sync the sprites of all bodies
local bodies = world:getBodies()
for i, body in ipairs(bodies) do
-- interpolate position
local x, y = body:getPosition()
local lvx, lvy = body:getLinearVelocity()
x = x + lvx*accumulator
y = y + lvy*accumulator
-- draw body
...
end
end
local contacts = body:getContacs() for i, contact in ipairs(contacts) do ... endor you can iterate all contacts:
local contacts = world:getContacts()Additionally a reference to the "Contact" object is provided when using collision callbacks.
Contact lists may contain potential collisions of fixtures that may not be touching at all. Using the "contact:IsTouching()" function tells us if there an actual collision.
function reg.Body:IsTouching(other)
-- iterate contacts
local contacts = self:getContacts()
for i, contact in ipairs(contacts) do
-- make sure there's actual contact
if contact:IsTouching() then
-- look for a specific body
local f1, f2 = contact:getFixtures()
if f1:getBody() == other or f2:getBody() == other then
return true
end
end
end
return false
end
Note that the code above returns true even if there is no solid contact.
Non-solid contact occurs when one or both of the contacting fixtures is a sensor.
Therefore, the approach shown above is pretty good if you want to add sensor triggers in your game.
A contact between two fixtures may have 2, 1 or 0 contact points.
As mentioned above, with non-solid contact (involving one or two sensor fixtures) there are 0 contact points.
When a circle collides with another fixture or a polygon vertex hits an edge, we always get 1 contact point.
When there is an edge-to-edge collision between two polygons, we may get 2 contact points.

Three different contacts with the contact points shown in white
Left: circle with 1 contact (1 point)
Center: triangle with 1 contact (1 point, vertex to edge)
Right: rectangle with 1 contact (2 points, edge to edge)
Keeping in mind that all fixtures in Box2D are convex,
it's easy to realize that there cannot be more than 2 contact points
between the same pair of fixtures.
However, one fixture may be in contact with two or more other fixtures.
Therefore a body can have several contacts acting upon it at the same time:
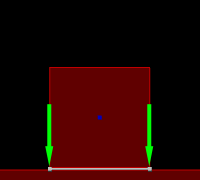
Four contacts with the contact points shown in white
Left: circle with 2 contacts (1 point each)
Right: rectangle with 2 contacts (1 point each)
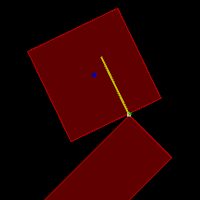
Another useful vector is the collision normal (see yellow lines in the figures above). Each contact has a collision normal which is basically the axis of shortest separation. In layman terms, it's a (normalized) vector describing the direction in which the two fixtures are pushing each other.
force = mass*acceleration acceleration = changeInVelocity/time changeInVelocity = finalVelocity - initialVelocityAn impulse is similar, but with "time" removed from the equation:
impulse = mass*changeInVelocity changeInVelocity = finalVelocity - initialVelocitySo you can think of an "impulse" as an instant change in velocity of an object times its mass.
Each contact point has an impulse associated with it.
Box2D describes the magnitude of these impulses in two parts.
The direction of these impulses is determined by the collision normal.
As you can see from the following figures,
normal impulses (shown in yellow) push the two fixtures apart so that
they are not inter-penetrating.
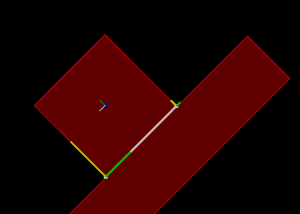
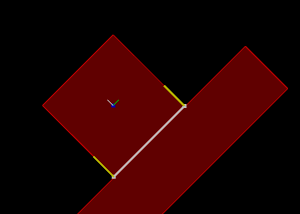
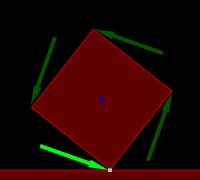
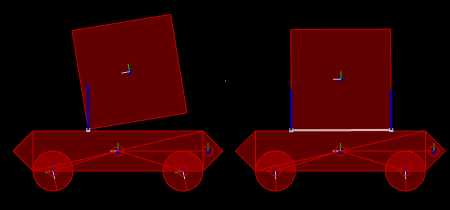
Rectangle going down an inclined slope.
Normal impulse shown in yellow and tangent impulse shown in green.
Left: with friction (1)
Right: without friction (0)
Tangent impulses are applied at 90-degrees relative to the "collision normal."
Tangent impulses are determined by the "friction" of fixtures and
can cause the body to spin and roll.
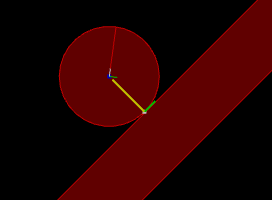
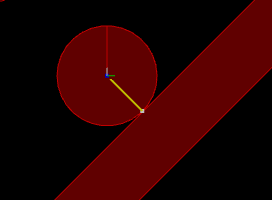
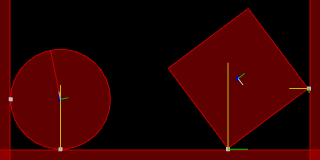
Circle going down an inclined slope.
Normal impulse shown in yellow and tangent impulse shown in green.
Left: with friction (1)
Center: without friction (0)
Remember: if you want your circles to roll make sure to give them a "friction" value greater than 0!
Otherwise, they will glide down awkwardly while remaining upright.
impulse = changeInVelocity*mass changeInVelocity = impulse/massKeep in mind that the exact point where an impulse is being applied is important too. The location of the contact point along with the center of mass of each body may produce torque and cause the body to spin.
Iterating the contact lists is great when you are interested in the "resting" contact between fixtures.
Sometimes however collisions may occur between frames.
If you want to know how much impulse is applied in such collisions,
you probably want to use a ContactListener with the "PostSolve" callback.
One downside is that the "PostSolve" callback may be evoked many times during a single update step.
I don't recommend "PostSolve" unless you need to know every impulse that is applied between fixtures.
function reg.Body:isMoving(treshold) treshold = treshold or 0 local lvx, lvy = self:getLinearVelocity() return (lvx*lvx + lvy*lvy) > treshold*treshold end
function reg.Body:isRotating(treshold) treshold = treshold or 0 local angular = self:getAngularVelocity() return angular < -treshold or angular > treshold end
function reg.Body:isMovingOnAxis(ax, ay) local lvx, lvy = self:getLinearVelocity(lv) return ax*lvx + ay*lvy > 0 end
function reg.Body:isPushedOnAxis(ax, ay)
local contacts = self:getContacts()
for i, contact in ipairs(contacts) do
if contact:isTouching() then
local x1, y1, x2, y2 = contact:getPositions()
if x1 and y1 then
local nx, ny = contact:getNormal()
local f1, f2 = contact:getFixtures()
local other = f1:getBody()
if other ~= self then
nx, ny = -nx, -ny
end
if ax*nx + ay*ny > 0 then
return true
end
end
end
end
return false
end
One further refinement could be to compute the total impulse acting on the body along the given axis.
This can help us determine how firmly the body is being supported.
restitution = contact:getRestitution()Depending on the restitution, we can categorize collisions in three types:
Perfectly elastic (restitution = 1)
No kinetic energy is lost so there is no sound or damage caused to the colliding objects.
Example: perfectly elastic ball that can bounce forever
Elastic (restitution > 0 and restitution < 1)
Some kinetic energy is converted into heat, sound or causes deformation.
Example: bouncing basketball
Inelastic (restitution = 0)
A lot of kinetic energy is converted into heat, sound or causes deformation.
The colliding objects remain together after the impact.
Example: ball made of soft clay that sticks to floor when dropped
Generally, momentum and energy are always conserved when dealing with a closed system. With Box2D, this is not particularly true for example when using static bodies with 0 restitution. Also note that, simulating deformation is beyond the scope of both Box2D and this tutorial.
As a general reference, let's look at the restitution coefficients of different types of balls:
0.858 golf ball
0.804 billiard ball
0.712 tennis ball
0.658 glass marble
0.597 steel ball bearing
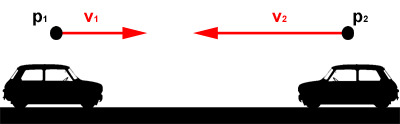
velocity1 = firstBody:getLinearVelocity() velocity2 = secondBody:getLinearVelocity() velocityDiff = velocity1 - velocity2Next, we find how fast the two bodies are moving towards each other, given the their difference in velocity and position.
-- direction vector direction = firstBody:getPosition() - secondBody:getPosition() directionNormal = normalize(direction) -- relative speed (in Meters per second) relativeSpeed = dotProduct(velocityDiff, directionNormal)The resulting relative speed is:
function preSolve(contact)
local x1, y1, x2, y2 = contact:getPositions()
if x1 and y1 then
local f1, f2 = contact:getFixtures()
local b1 = f1:getBody()
local b2 = f2:getBody()
-- Campbell's method
local lvx1, lvy1 = b1:getLinearVelocityFromWorldPoint(x1, y1)
local lvx2, lvy2 = b2:getLinearVelocityFromWorldPoint(x1, y1)
-- velocity difference vector
local dvx, dvy = lvx1 - lvx2, lvy1- lvy2
-- impact speed (in Meters per second)
local nx, ny = contact:getNormal()
local impactSpeed = dvx*nx + dvy*ny -- dot product
When used in the "PreSolve" callback,
the result is the relative speed of the contact points
at the moment of impact!
When we know the impact speed it's possible to estimate the impulse which
will later be applied to the body during the "PostSolve" callback.
Again, remember that impact speed is actually the relative velocity of the points in contact.
When torque is involved, it could be different than the linear velocity of the body.