Collision detection and intersections

Introduction

This is going to be a brief tutorial on collision detection. Before we can dive in the intersection algorithms, let's look at some basic geometry operations.

Rectangle representations

Note that in any example involving rectangles, we will deal with several implementations because rectangles could be represented in a number of ways.

The same rectangle represented in three different ways

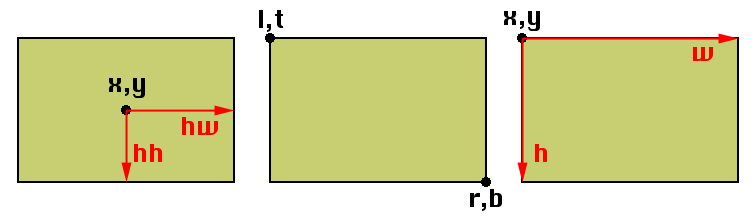
Box (center point with half-width and half-height extents)
One way to represent rectangles is as a center point (x, y) with half-width and half-height extents (hw, hh). This is very useful when programming games, because it's generally easier to work with the centers of collisions shapes. Also, it's easier to include rotation or other transformations to the rectangle when its origin is at the center.

AABB (left, top, right, bottom)
A second implementation treats rectangles as four numbers (l, t, r, b) where (l, t) is the top-left corner and (r, b) is the bottom-right corner.

Rect (top-left point with width and height dimensions)
The last example represent rectangles as a top-left corner point (x, y) with width and height dimensions (w, h).

Nearest point

Given an arbitrary position (P) outside of a shape, we want to find the nearest point (P₂) on that shape. If P is already inside the area of the shape, the algorithms return the original point P. The nearest point algorithms can be used to solve more complicated intersection tests.

Nearest point on a segment

Given a line segment (x1, y1, x2, y2) we find the nearest point P₂ on that segment from position P. The result is obtained using two dot products "cx*dx + cy*dy" and "dx*dx + dy*dy". One caveat is that if the segment is degenerate (has zero length) a division by zero will occur. That's why we need the check if "d == 0". One modification could be to remove the two if/else statements "if u < 0" and "elseif u > 1" and then the segment (x1, y1, x2, y2) will be treated as an infinite line.

function pointOnSegment(px, py, x1, y1, x2, y2)
  local cx, cy = px - x1, py - y1
  local dx, dy = x2 - x1, y2 - y1
  local d = (dx*dx + dy*dy)
  if d == 0 then
    return x1, y1
  end
  local u = (cx*dx + cy*dy)/d
  if u < 0 then
    u = 0
  elseif u > 1 then
    u = 1
  end
  return x1 + u*dx, y1 + u*dy
end

Example 1: Nearest point on a line segment

Nearest point on a circle

Another common operation is finding the nearest point P₂ in the circle area from an arbitrary position P. Note that the original point is returned if P is already inside the circle.

function pointOnCircle(px, py, cx, cy, r)
  local dx, dy = px - cx, py - cy
  local d = math.sqrt(dx*dx + dy*dy)
  if d <= r then
    return px, py
  end
  return dx/d*r + cx, dy/d*r + cy
end

Example 2: Nearest point on a circle

Nearest point on a rectangle

Given an arbitrary point P the following function finds the nearest point P₂ in the area of the rectangle. The code simply clamps the given point P to the extents of the rectangle. This example is designed for axis-aligned rectangles. For rotated rectangles, the point P needs to be translated relative to the center of the rectangle and then rotated.

function pointOnBox(px, py, x, y, hw, hh)
  local qx, qy = px - x, py - y
  if qx > hw then
    qx = hw
  elseif qx < -hw then
    qx = -hw
  end
  if qy > hh then
    qy = hh
  elseif qy < -hh then
    qy = -hh
  end
  return qx + x, qy + y
end

function pointOnAABB(px, py, l, t, r, b)
  if px < l then
    px = l
  elseif px > r then
    px = r
  end
  if py < t then
    py = t
  elseif py > b then
    py = b
  end
  return px, py
end

function pointOnRect(px, py, l, t, w, h)
  px = math.max(px, l)
  px = math.min(px, l + w)
  py = math.max(py, t)
  py = math.min(py, t + h)
  return px, py
end

Example 3: Nearest point on a rectangle

Nearest point on a triangle

The following example finds the nearest point on a triangle using Barycentric coordinates.

local function dot(ax, ay, bx, by)
  return ax*bx + ay*by
end
function pointOnTriangle(px, py, ax, ay, bx, by, cx, cy)
  local abx, aby = bx - ax, by - ay
  local acx, acy = cx - ax, cy - ay
  local apx, apy = px - ax, py - ay
  -- vertex region outside a
  local d1 = dot(abx, aby, apx, apy)
  local d2 = dot(acx, acy, apx, apy)
  if d1 <= 0 and d2 <= 0 then
    return ax, ay
  end
  -- vertex region outside b
  local bpx, bpy = px - bx, py - by
  local d3 = dot(abx, aby, bpx, bpy)
  local d4 = dot(acx, acy, bpx, bpy)
  if d3 >= 0 and d4 <= d3 then
    return bx, by
  end
  -- edge region ab
  if d1 >= 0 and d3 <= 0 and d1*d4 - d3*d2 <= 0 then
    local v = d1/(d1 - d3)
    return ax + abx*v, ay + aby*v
  end
  -- vertex region outside c
  local cpx, cpy = px - cx, py - cy
  local d5 = dot(abx, aby, cpx, cpy)
  local d6 = dot(acx, acy, cpx, cpy)
  if d6 >= 0 and d5 <= d6 then
    return cx, cy
  end
  -- edge region ac
  if d2 >= 0 and d6 <= 0 and d5*d2 - d1*d6 <= 0 then
    local w = d2/(d2 - d6)
    return ax + acx*w, ay + acy*w
  end
  -- edge region bc
  if d3*d6 - d5*d4 <= 0 then
    local d43 = d4 - d3
    local d56 = d5 - d6
    if d43 >= 0 and d56 >= 0 then
      local w = d43/(d43 + d56)
      return bx + (cx - bx)*w, by + (cy - by)*w
    end
  end
  -- inside face region
  return px, py
end

Example 4: Nearest point on a triangle

Point inside shape

Given an arbitrary point P we want to test if it lies inside the area of a given shape.

Point inside circle

Testing if a point is inside a circle is a two-step algorithm. First, we subtract the given point from the center of the circle. Next, we compare the length of the resulting vector to the radius of the circle. As an optimization, we avoid math.sqrt by comparing the square length and the square radius (r^2 or r*r).

function pointInCircle(px, py, cx, cy, r)
  local dx, dy = px - cx, py - cy
  return dx*dx + dy*dy <= r*r
end

Example 5: Point vs circle
P: point being tested
C: circle center

Point inside rectangle

This is a relatively simple and inexpensive algorithm that checks each axis for overlap. Note that the second implementation (AABB) is the fastest and works entirely by comparing numbers.

function pointInBox(px, py, x, y, hw, hh)
  if math.abs(px - x) > hw then
    return false
  end
  if math.abs(py - y) > hh then
    return false
  end
  return true
end

function pointInAABB(px, py, l, t, r, b)
  if px < l or px > r then
    return false
  end
  if py < t or py > b then
    return false
  end
  return true
end

function pointInRect(px, py, l, t, w, h)
  if px < l or px > l + w then
    return false
  end
  if py < t or py > t + h then
    return false
  end
  return true
end

Example 6: Point in rectangle

Point inside triangle

This simple algorithm is based on an example discussed by Christer Ericson in his book. The way the code works is by checking on which "side" the point P is located, in relation to each edge of the triangle.

function pointInTriangle(px, py, x1, y1, x2, y2, x3, y3)
  local ax, ay = x1 - px, y1 - py
  local bx, by = x2 - px, y2 - py
  local cx, cy = x3 - px, y3 - py
  local sab = ax*by - ay*bx < 0
  if sab ~= (bx*cy - by*cx < 0) then
    return false
  end
  return sab == (cx*ay - cy*ax < 0)
end

Example 7: Point in triangle

Overlap checks

Given two shapes, we want to find if they intersect. For performance reasons, functions that detect if two shapes are intersecting should be programmed to return "false" as soon as possible.

Segment vs segment

The following function checks if two line segments (x1, y1, x2, y2 and x3, y3, x4, y4) are intersecting. The code uses two cross product "dx2*dy3 - dy2*dx3" and "dx1*dy3 - dy1*dx3" divided by a determinant (d). Note that the first check "if d == 0" returns false when the segments are either collinear or degenerate.

function segmentVsSegment(x1, y1, x2, y2, x3, y3, x4, y4)
  local dx1, dy1 = x2 - x1, y2 - y1
  local dx2, dy2 = x4 - x3, y4 - y3
  local dx3, dy3 = x1 - x3, y1 - y3
  local d = dx1*dy2 - dy1*dx2
  if d == 0 then
    return false
  end
  local t1 = (dx2*dy3 - dy2*dx3)/d
  if t1 < 0 or t1 > 1 then
    return false
  end
  local t2 = (dx1*dy3 - dy1*dx3)/d
  if t2 < 0 or t2 > 1 then
    return false
  end
  -- point of intersection
  return true, x1 + t1*dx1, y1 + t1*dy1
end

Example 8: Segment vs segment

Segment vs circle

Given any line segment we want to find if it intersects a circle defined by a specific position and radius.

local function segmentVsCircle(x1, y1, x2, y2, cx, cy, cr)
  local qx, qy = pointOnSegment(cx, cy, x1, y1, x2, y2)
  return pointInCircle(qx, qy, cx, cy, cr)
end

Expanded version that finds the points of intersection:

function segmentVsCircle(x1, y1, x2, y2, cx, cy, cr)
  -- normalize segment
  local dx, dy = x2 - x1, y2 - y1
  local d = math.sqrt(dx*dx + dy*dy)
  if d == 0 then
    return false
  end
  local nx, ny = dx/d, dy/d
  local mx, my = x1 - cx, y1 - cy
  local b = mx*nx + my*ny
  local c = mx*mx + my*my - cr*cr
  if c > 0 and b > 0 then
    return false
  end
  local discr = b*b - c
  if discr < 0 then
    return false
  end
  discr = math.sqrt(discr)
  local tmin = math.max(-b - discr, 0)
  if tmin > d then
    return false
  end
  local tmax = math.min(discr - b, d)
  -- points of intersection
  -- first point
  local qx, qy = x1 + tmin*nx, y1 + tmin*ny
  if tmax == tmin then
    return true, qx, qy
  end
  -- second point
  return true, qx, qy, x1 + tmax*nx, y1 + tmax*ny
end

Example 9: Segment vs circle

Segment vs rectangle

Note that the following example works only for axis-aligned rectangles.

function segmentVsAABB(x1, y1, x2, y2, l, t, r, b)
  -- normalize segment
  local dx, dy = x2 - x1, y2 - y1
  local d = math.sqrt(dx*dx + dy*dy)
  if d == 0 then
    return false
  end
  local nx, ny = dx/d, dy/d
  -- minimum and maximum intersection values
  local tmin, tmax = 0, d
  -- x-axis check
  if nx == 0 then
    if x1 < l or x1 > r then
      return false
    end
  else
    local t1, t2 = (l - x1)/nx, (r - x1)/nx
    if t1 > t2 then
      t1, t2 = t2, t1
    end
    tmin = math.max(tmin, t1)
    tmax = math.min(tmax, t2)
    if tmin > tmax then
      return false
    end
  end
  -- y-axis check
  if ny == 0 then
    if y1 < t or y1 > b then
      return false
    end
  else
    local t1, t2 = (t - y1)/ny, (b - y1)/ny
    if t1 > t2 then
      t1, t2 = t2, t1
    end
    tmin = math.max(tmin, t1)
    tmax = math.min(tmax, t2)
    if tmin > tmax then
      return false
    end
  end
  -- points of intersection
  -- one point
  local qx, qy = x1 + nx*tmin, y1 + ny*tmin
  if tmin == tmax then
    return true, qx, qy
  end
  -- two points
  return true, qx, qy, x1 + nx*tmax, y1 + ny*tmax
end

Example 10: Segment vs rectangle

Circle vs circle

By adding the radii of the two circles, we can treat one of the circles as a point.

function circleVsCircle(cx, cy, r, cx2, cy2, r2)
  return pointInCircle(cx, cy, cx2, cy2, r + r2)
end

Expanded version:

function circleVsCircle(cx, cy, r, cx2, cy2, r2)
  local sradii = r + r2
  local dx, dy = px - cx, py - cy
  return dx*dx + dy*dy <= sradii*sradii
end

Example 11: Circle vs circle
C₁: center of the first circle
C₂: center of the second circle
d: vector from the center of the first circle to the center of the second circle where d = C₂ - C₁. The two circles cannot overlap if the length of d is greater than the sum of the radii.

Circle vs rectangle

First, we find the nearest point on the rectangle to the circle center, then we compare the distance to the circle radius. Another way to describe the problem could be as finding if a point is inside a "rounded" rectangle.

function circleVsBox(cx, cy, cr, x, y, hw, hh)
  local qx, qy = pointOnBox(cx, cy, x, y, hw, hh)
  return pointInCircle(qx, qy, cx, cy, cr)
end

Expanded version:

function circleVsBox(cx, cy, cr, x, y, hw, hh)
  local dx = math.abs(x - cx)
  local dy = math.abs(y - cy)
  dx = math.max(dx - hw, 0)
  dy = math.max(dy - hh, 0)
  return dx*dx + dy*dy <= cr*cr
end

local function clamp(n, min, max)
  if n < min then
    n = min
  elseif n > max then
    n = max
  end
  return n
end
function circleVsAABB(cx, cy, cr, l, t, r, b)
  local dx = clamp(cx, l, r) - cx
  local dy = clamp(cy, t, b) - cy
  return dx*dx + dy*dy <= cr*cr
end

local function clamp(n, min, max)
  if n < min then
    n = min
  elseif n > max then
    n = max
  end
  return n
end
function circleVsRect(cx, cy, cr, l, t, w, h)
  local dx = clamp(cx, l, l + w) - cx
  local dy = clamp(cy, t, t + h) - cy
  return dx*dx + dy*dy <= cr*cr
end

Example 12: Rectangle vs circle
C: circle center
R: rectangle center
P: nearest point from C to the edges of the rectangle

Circle vs triangle

First, we project the center of the circle C to the edges of the triangle. Once we have found the projected point P, the rest of the code becomes trivial.

function triangleVsCircle(ax, ay, bx, by, cx, cy, sx, sy, r)
  local qx, qy = pointOnTriangle(sx, sy, ax, ay, bx, by, cx, cy)
  return pointInCircle(qx, qy, sx, sy, r)
end

Example 13: Triangle vs circle
C: center of the circle
P: nearest point from the center of the circle to the edges of the triangle

Rectangle vs rectangle

The rectangle vs rectangle test checks each axis and returns false if there cannot be an intersection. Again, the second implementation (AABB) is the fastest although the parameters must be aligned so that: l < r and t < b and l2 < r2 and t2 < b2.

function boxVsBox(x, y, hw, hh, x2, y2, hw2, hh2)
  if math.abs(x - x2) > hw + hw2 then
    return false
  end
  if math.abs(y - y2) > hh + hh2 then
    return false
  end
  return true
end

function AABBVsAABB(l, t, r, b, l2, t2, r2, b2)
  if l > r2 or l2 > r then
    return false
  end
  if t > b2 or t2 > b then
    return false
  end
  return true
end

function rectVsRect(l, t, w, h, l2, t2, w2, h2)
  if l > l2 + w2 or l2 > l + w then
    return false
  end
  if t > t2 + h2 or t2 > t + h then
    return false
  end
  return true
end

Example 14: Rectangle vs rectangle
dx, dy: x-axis and y-axis distances from the center of the first rectangle (R₁) to the center of the second rectangle (R₂) where dx = R₂.x - R₁.x and dy = R₂.y - R₁.y. The two rectangles cannot overlap if abs(dx) is greater than the sum of the half-width extents (hw + hw2) or if abs(dy) is greater than the sum of the half-height extents (hh + hh2).

Triangle vs triangle

The following algorithm checks if all of the vertices of one triangle lie on the same side of any edge from the other triangle. If such edge exists, we know that the two triangles cannot overlap.

local function cross2(x1,y1,x2,y2,x3,y3, ax,ay,bx,by,cx,cy) {
  local dXa, dYa = ax - x3, ay - y3
  local dXb, dYb = bx - x3, by - y3
  local dXc, dYc = cx - x3, cy - y3
  local x32, y23 = x3 - x2, y2 - y3
  local x13, y13 = x1 - x3, y1 - y3
  local D = y23*x13 + x32*y13
  local sa = y23*dXa + x32*dYa
  local sb = y23*dXb + x32*dYb
  local sc = y23*dXc + x32*dYc
  if D < 0 then
    if sa >= 0 and sb >= 0 and sc >= 0 then
      return true
    end
    local ta = x13*dYa - y13*dXa
    local tb = x13*dYb - y13*dXb
    local tc = x13*dYc - y13*dXc
    return (ta >= 0 and tb >= 0 and tc >= 0)
      or (sa+ta <= D and sb+tb <= D and sc+tc <= D))
  else
    if sa <= 0 and sb <= 0 and sc <= 0 then
      return true
    end
    local ta = x13*dYa - y13*dXa
    local tb = x13*dYb - y13*dXb
    local tc = x13*dYc - y13*dXc
    return (ta <= 0 and tb <= 0 and tc <= 0)
      or (sa+ta >= D and sb+tb >= D and sc+tc >= D)
  end
end

function triangleVsTriangle(x1,y1,x2,y2,x3,y3, ax,ay,bx,by,cx,cy)
  return not (cross2(x1,y1,x2,y2,x3,y3, ax,ay,bx,by,cx,cy) or
    cross2(ax,ay,bx,by,cx,cy, x1,y1,x2,y2,x3,y3))
end

Example 15: Triangle vs triangle

References

Realtime Collision Detection by Christer Ericson
Path by Cosmin Apreutesei
StackOverflow answer by Hassan Nadeem