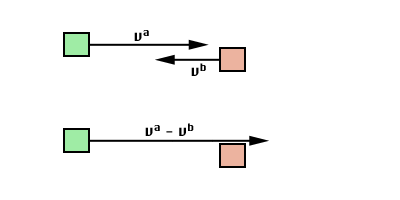
Subtracting the velocities of objects a and b allows us to treat shape b as if it is stationary.
velocity = velocity + gravity*dt position = position + velocity*dtThese calculations are performed during each step of the simulation for every moving (dynamic) object. For practical reasons, it's useful to limit the velocity of moving objects to a certain threshold (maxVelocity). It's also common in games to have non-moving or static objects. Static objects are not affected by gravity or collisions and can be used to represent platforms, walls and so on.
-- updates the simulation
function update(dt)
-- update velocity vectors
local grav = gravity*dt
for i = 1, #dynamics do
local d = dynamics[i]
-- gravity
d.yv = d.yv + grav
d.xv, d.yv = clampVec(d.xv, d.yv, maxVelocity)
end
-- move dynamic objects
for i = 1, #dynamics do
local d = dynamics[i]
moveShape(d, d.xv*dt, d.yv*dt)
-- check and resolve collisions
for j, s in ipairs(statics) do
checkCollision(d, s)
end
for j = i + 1, #dynamics do
checkCollision(d, dynamics[j])
end
end
end
The technique can be summed up as:
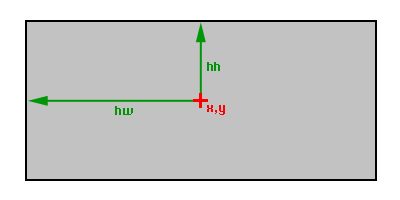
function testRectRect(a, b)
-- distance between the rects
local dx, dy = a.x - b.x, a.y - b.y
local adx = math.abs(dx)
local ady = math.abs(dy)
-- sum of the extents
local shw, shh = a.hw + b.hw, a.hh + b.hh
if adx >= shw or ady >= shh then
-- no intersection
return
end
-- intersection
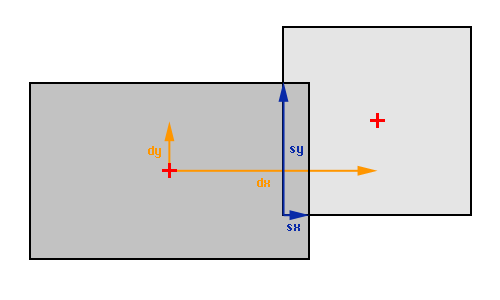
-- shortest separation
local sx, sy = shw - adx, shh - ady
-- ignore longer axis
if sx < sy then
if sx > 0 then
sy = 0
end
else
if sy > 0 then
sx = 0
end
end
-- correct sign
if dx < 0 then
sx = -sx
end
if dy < 0 then
sy = -sy
end
return sx, sy
end
The separation vector gives us two important pieces of information
about the intersecting shapes:
-- checks for collision
function checkCollision(a, b)
local sx, sy = testRectRect(a, b)
if sx and sy then
solveCollision(a, b, sx, sy)
end
end
-- resolves collision
function solveCollision(a, b, sx, sy)
-- find the collision normal
local d = math.sqrt(sx*sx + sy*sy)
local nx, ny = sx/d, sy/d
-- relative velocity
local vx, vy = a.xv - (b.xv or 0), a.yv - (b.yv or 0)
-- penetration speed
local ps = vx*nx + vy*ny
-- objects moving towards each other?
if ps <= 0 then
-- separate the two objects
moveShape(a, sx, sy)
end
end
First, we subtract the velocities of the two objects.
This gives us the relative velocity during impact.

Subtracting the velocities of objects a and b allows
us to treat shape b as if it is stationary.
-- resolves collision function solveCollision(a, b, sx, sy) -- find the collision normal local d = math.sqrt(sx*sx + sy*sy) local nx, ny = sx/d, sy/d -- relative velocity local vx, vy = a.xv - (b.xv or 0), a.yv - (b.yv or 0)Next, we have to figure out how the moving shape should react to the collision (bounce, slide or stop completely). This is done be splitting the relative velocity into penetration and tangent components.
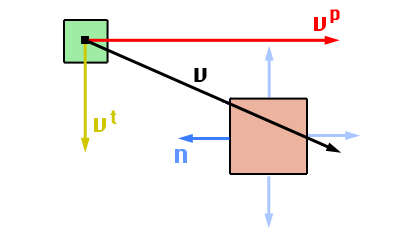
The dot product (ps) between the relative velocity and the collision normal (vx*nx + vy*ny) gives us the speed at which the two objects are moving toward each other. This product (ps) may be positive or negative depending on whether the objects are moving apart or toward each other.
-- penetration speed local ps = vx*nx + vy*ny -- objects moving apart? if ps > 0 then return end -- penetration component local px, py = nx*ps, ny*psUsually, we calculate the tangent component by rotating the collision normal 90 degrees and using the dot product:
-- tangent speed local ts = vx*ny - vy*nx -- tangent component local tx, ty = ny*ts, -nx*tsHowever, since we already know the penetration speed (ps) and velocity (px, py) at which the two objects are colliding, we can just subtract it from the relative velocity (vx, vy):
-- penetration speed local ps = vx*nx + vy*ny -- penetration component local px, py = nx*ps, ny*ps -- tangent component local tx, ty = vx - px, vy - py
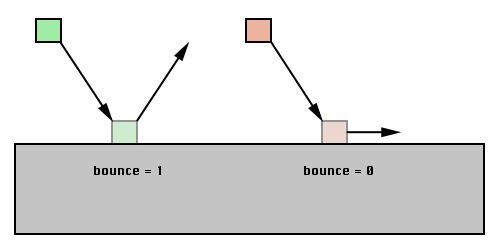
-- penetration speed local ps = vx*nx + vy*ny -- penetration component local px, py = nx*ps, ny*ps -- restitution local r = 1 + math.max(a.bounce, b.bounce or 0) -- change the velocity of shape a a.xv = a.xv - px*r a.yv = a.yv - py*r
-- penetration speed local ps = vx*nx + vy*ny -- penetration component local px, py = nx*ps, ny*ps -- tangent component local tx, ty = vx - px, vy - py -- restitution local r = 1 + math.max(a.bounce, b.bounce or 0) -- friction local f = math.min(a.friction, b.friction or 0) -- change the velocity of shape a a.xv = a.xv - px*r + tx*f a.yv = a.yv - py*r + ty*fFinaly, we multiply the penetration component by the restitution (r), the tangent component by the friction (f) and add them together to get the resulting change in velocity of the moving shape.
-- how mass affects impulse ChangeInVelocity = FinalVelocity - InitialVelocity Impulse = Mass*ChangeInVelocity -- how mass affects momentum Momentum = Velocity*Mass -- how mass affects force Acceleration = ChangeInVelocity/Time Force = Mass*Acceleration